- أنواع المثلثات
- ما هي أنواع المثلثات؟
- تختلف أنواع الزوايا حسب أضلاعها
- تصنيف المثلثات حسب الزوايا الداخلية
- أمثلة على قياس الزوايا للمثلث
أنواع المثلثات
المثلث عبارة عن شكل هندسي يتكوّن من ثلاثة أضلاع رئيسية، قاعدة وضلعين، والنقاط المكوّنة لعملية التقاء هذه الأضلاع تسمى برؤوس المثلث، هذا ببساطة هو تعريف هذا الشكل الهندسي الهام، وببساطة أكثر فإن هناك العديد من الجوانب الهندسية حول خصائص وأنواع المثلثات، هذا إلى جانب قياس الزوايا المختلفة، وتطبيقات هذا على الناحية الحسابية لمساحة المثلث طول أضلاعه وغيرها من المعلومات الهندسية الممتعة، وكل هذا نتعرف عليه خلال السطور القليلة القادمة.
ما هي أنواع المثلثات؟
كما قلنا في المقدمة، فإن المثلث عبارة عن شكل هندسي له العديد من الخصائص الحسابية، ولكن نركز في هذه النقطة حول أنواع هذه المثلثات، فما هي أنواعه؟
يقسّم العلماء في مجال الرياضيات والهندسة منذ القدم المثلثات إلى ثلاثة أنواع حسب الزوايا وحساب هذه الزاوية، والتقسيمات كالتالي، وهم مثلث حاد الزاوية، ومثلث قائم الزاوية، ومثلث منفرج الزاوية، وسنتعرف من خلال النقاط التالية العديد من التفاصيل الهندسية الهامة لكل من هذه المثلثات كل على حدة:
المثلث حاد الزاوية
وهو المثلث الذي يقل قياس زواياه الثلاثة عن 90 درجة في القياس الهندسي، يعني على سبيل المثال مثلث عدد زواياه 60 درجة، فهذا يسمى بمثلث حاد الزاوية، وهكذا، طالما لم يصل إلى 90 درجة، يبقى المثلث بأضلاعه وزواياه من النوع الحاد.
المثلث قائم الزاوية
وهو أن يكون هذا المثلث عند زاوية واحدة في القاعدة أو في أي ضلع من الأضلاع الثلاثة يساوي 90 درجة، حتى لو كان زاوية من ضمن الزوايا الثلاثة حادة، فيبقى الزاوية الأساسية قائمة طالما وصلت لدرجة القياس الهندسي إلى 90 درجة.
المثلث منفرج الزاوية
وهذا المثلث لابد أن يصل زاوية من زواياه للحالة المنفرجة، وهي أن يكون القياس الهندسي للزاوية تلك أكبر من 90 درجة، حتى لو كان الزاوية الأولى حادة، والثانية قائمة، فالثالثة لابد وأن تكون منفرجة القياس، وبالتالي يكون المثلث منفرج الزاوية.
تختلف أنواع الزوايا حسب أضلاعها
إذا تعرفنا في النقاط السابقة على أنواع الزوايا حسب الزاوية وقياسها، فإن هناك أنواع أخرى حول أضلاع المثلث، فإن هذه الأنواع هي:
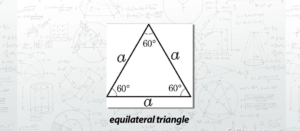
مثلث متساوي الأضلاع
هذا المثلث يتساوى معه أضلاع المثلث في الطول، وهذا ينتج عنه ثلاث زوايا متساوية في القياس، حيث يوجد لكل زاوية قياس هندسي عند الدرجة 60، وبالتالي فإن هذا هو المثلث المتساوي في الأضلاع وينتج عنه تساوي الزوايا أيضاً.
مثلث متساوي الضلعين
يطلق أيضاً عليه المثلث متساوي الساقين، وهو عبارة عن مثلث يتكون من ضلعين متساويين في الطول وينتج عن هذا التساوي زاويتان متساويتان في القياس، وتتمثلان للزاويتين المجاورتين للضلعين المتساويين وفي نفس الوقت نفسه زوايتا قاعدة المثلث.
مثلث مختلف الأضلاع
وهذا النوع من المثلثات به ثلاثة أضلاع مختلفين في قياسهما من حيث الطول، وينتج عنه اختلاف قياس الزوايا عند كل ضلع من هذا المثلث.
تصنيف المثلثات حسب الزوايا الداخلية
الزوايا الداخلية بالطبع يمكن معرفة أنواع المثلثات من خلالها، وهذه عبارة عن أمثلة سنتعرف من خلالها كيفية تصنيف أنواع المثلثات المختلفة حسب الزوايا الداخلية، وهذه الأمثلة التي نتعرف عليها من خلال النقاط التالية:
- مثلث قياس الزوايا الداخلية له تساوي ( 50 ، 70، 60) فإن هذا النوع مثلث حاد الزوايا، وذلك لأن الزوايا جميعها أقل من 90 درجة، وبالتالي فإنه أيضاً مثلث مختلف الأضلاع حسب التصنيف حول الأضلاع والذي تعرفنا عليه.
- مثلث قياس أطوال أضلاعه ما بين 9 – 6 – 4 سم: هذا مثلث مختلف الاضلاع، وذلك لأن طول كل ضلع على حدة مختلف عن الآخر، وبالتالي فإنه يسمى بمثلث مختلف الزوايا.
- مثلث قياس الزوايا الداخلية ما بين 90- 50 – 40 درجة: هذا يعني أنه مثلث قائم الزاوية، وذلك لأن زاوية من ضمن زواياه الثلاثة تساوي 90 درجة، ومع ذلك فهو مختلف الأضلاع.
- مثلث قياس الزوايا الثلاثة فيه ما بين 120 – 30 – 35: هذا مثلث منفرج الزاوية، وذلك لأن زاوية من ضمن زواياه الثلاثة، تساوي 120 أي أعلى من الزاوية القائمة 90 درجة.
- مثلث قياس أضلاعه الثلاثة ما بين 4 – 4 – 9 سم: هذا مثلث متساوي الساقين، وذلك لأن ضلعين منه نفس الطول وهو 4 سم، بينما القاعدة 9سم، وبالتالي فإن زاويتين من مجموع الزوايا الثلاثة متساويان في الدرجة بينما تختلف الثالثة عنهما.
- مثلث قياس أطوال أضلاعه الثلاثة ما بين ( 4 – 4 – 4 م): في هذه الحالة، فإنه مثلث متساوي الأضلاع، وبالتالي فهو متساوي الزوايا ايضاً.
- مثلث قياس الزوايا الداخلية فيه ما بين ( 122- 22- 15 درجة ): هذا مثلث منفرج الزوايا الداخلية، وذلك من أجل احتوائه على زاوية قياسها أكبر من 90 درجة، وبالتالي فهو منفرج، وفي نفس الوقت فهو مثلث مختلف الأضلاع.
أمثلة على قياس الزوايا للمثلث
لكي نفهم المعلومات الهندسية السابقة، فإننا سنتعرف على بعض الأمثلة الهامة للشكل الهندسي المثلث، من خلال قياس الزوايا الداخلية له، وهذا ما نتعرف عليه خلال الامثلة التالية:
المثال الأول
في حالة كانت النسبة بين الزوايا الثلاث للمثلث هي 1:2:3 فما هو نوع هذا الشكل المثلثي؟
الحل
نقوم بقياس إحدى الزوايا وليكن الزاوية س وتكون الزاويتين المتبقيتين في المثلث هما 2 س ، 3 س ومن خلال ذلك فإن مجموع زوايا المثلث = 180 درجة، و بقسمة الطرفين على 6 فهو ينتج أن س = 30 وذلك من خلال المعادلة الحسابية التالية: س+2س+3س=180
وبالتالي فإن حساب قياس الزوايا هي كالتالي:
- الزاوية الأولى= س= 30 درجة.
- الزاوية الثانية= 2 س = 2 × 30 = 60 درجة.
- الزاوية الثالثة: 3 س = 3 × 30 = 90 درجة.
وبالتالي فإن المثلث هذا قائم الزاوية، وذلك لأن قياس إحدى زواياه الداخلية تساوي 90 درجة.
المثال الثاني:
إذا كانت قياس إحدى الزوايا المتساوية في المثلث متساوي الساقين 50 درجة، فما هو قياس الزاويتين المتبقيتين في هذا المثلث؟
الحل: قياس الزاويتين المتساويتين = 50، وعملية طرح قياس الزاويتين من مجموع الزوايا في المثلث فإن قياس الزاوية الثالثة هو: 180- ( 50 – 50) = 80 درجة، وذلك لأن مجموع الزوايا لأي مثلث هو 180 درجة وبالتالي فإنه يتم الطرح من المجموع الكلي لهذه الزوايا.
المثال الثالث:
إذا كانت زاوية مثلث متساوي الأضلاع هو: 3س+12، 4 س+8، 6 س فما هو طول كل منهما؟
الحل: في البداية يتم تعريف المثلث متساوي الأضلاع من خلال 3س+12=6س، ومنه: س=4 وبالتالي فإن طول كل ضلع من الأضلاع في هذا المثلث = 6 س = 4 × 6 = 24 سم.
أنواع المثلثات كما تناولناها في السطور السابقة عديدة حسب الزوايا أو تصنيفات أخرى حسب الأضلاع وقياسها، لذلك قمنا بعرض هذه الأنواع مع معلومات هندسية أخرى تدل على اهمية المثلث في عالم الهندسة الممتع.
بواسطة: Asmaa Majeed




























































اضف تعليق